
Celebrate ten years of Urban Omnibus and support ten more years of fresh, independent perspectives on citymaking with a donation today!
Celebrate ten years of Urban Omnibus and support ten more years of fresh, independent perspectives on citymaking with a donation today!
122 years ago today, on March 11th 1888, it started snowing. When the snows finally came to a stop three days later, over forty inches were reported in New York and New Jersey and some snowdrifts grew as high as 50 feet. All major cities between Washington and Montreal were completely isolated from each other. The damage was so severe – collapsing wires caused fires, melting snow caused floods, at least 400 people lost their lives – that as soon as New Yorkers dug themselves out of what came to be called “The Great White Hurricane” they went about ensuring that no future weather event would cause as much injury, death or destruction to property and livelihoods. One of this legislative regime’s longest-lasting legacies is its effect on mass transit.
Among the laws enacted that year, one prohibited catenary in Manhattan, meaning no more overhead lines were permitted to transmit electricity to trams, trolleys and buses. Some argue that the storm is what pushed Northeastern cities to finally move ahead with plans to start building public transit underground (Boston’s subway, the first in the nation, opened nine years after the storm). That law is still in effect, which still hampers the City’s ability to install light rail or certain kinds of electrical bus systems.
Over the past few months, the City has been looking at a number of different options – including light rail and streetcars – for improving mass transit service in Midtown Manhattan. And in last week’s roundup, we relayed the news that the DOT plan for Midtown includes dedicating a bus lane, or transitway, along 34th Street river to river. By invoking the precedents of Curitiba and Bogotá, we implied that this move signifies Manhattan’s first foray into the world of Bus Rapid Transit, or BRT. Yonah Freemark at The Transport Politic has a comprehensive analysis of why, for better or worse, BRT is not the most accurate way to characterize the transitway, and he also makes reference to the 1888 law about overhead wiring. To be sure, the plan will speed up the journey considerably. But the project says more about the priority DOT places on improving pedestrian experience of the street than it does about the DOTs willingness to experiment with more efficient modes of transit. “Despite the fact that the DOT has been on an all-out crusade to improve bus service, has no money for more subways, and has demonstrated little interest in light rail or streetcars, it evaluated all four in its recent study for the 34th Street corridor.” Its recommendation to create a dedicated bus lane, which is cheaper than the alternatives (“between $30 and 125 million, versus $250 million and up for light rail or several billion for a full-scale subway line”), is not about making bus service rapid. “With 13 stations end to end — roughly every 800 feet — buses will average a miserable six miles per hour, hardly faster than a person can walk the route.” It’s about improving “the streetscape for pedestrians, who until recently have been put in last place by New York City decision-making.”
Earlier this week, the Omnibus continued its look at how standards and codes, inflexible by nature – such as the code prohibiting living units in cellars – may be developed in the public interest but are often enforced at the public’s expense. In other words, if we don’t continuously evaluate how technological, cultural and demographic shifts change the way people live, urban development will continue to outpace governance. I’m not saying we should insist on a return of overhead wires. But we should certainly arm ourselves, as concerned urban citizens, with the knowledge of where the laws that limit urban innovation originate.
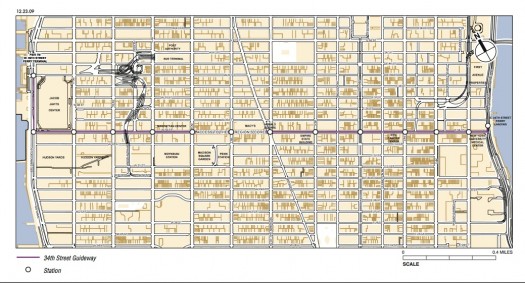
Map of proposed bus transit along 34th Street, from New York City DOT.
The views expressed here are those of the authors only and do not reflect the position of The Architectural League of New York.